Solving Equations I
Definitions:
Equation => a mathematical statement that consists of two expressions
joined by an equal sign, =.
False statements
1 + 2 = 4
True statements
1 + 2 = 3
Conditionally true statements x + 2 = 3 (conditional equation)
If the value of x is 1, this equation is true. Otherwise, this equation is
false.
Linear equation in one variable: ax + b = c, where a, b, and c are real
numbers. Where a ≠ 0, and x is a variable that
represents an unknown quantity. In a linear equation, the variable always has
exponent 1.
A linear equations can not have a variable under a radical or in the
denominator.
Linear equations can only have 1 variable.
Examples:
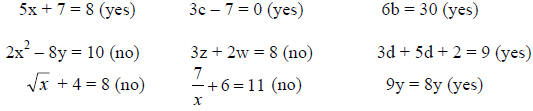
NOTICE:
| Expression |
Equation |
| Never contains an equal sign |
always contains an equal sign |
| Simplify an expression |
solve an equation |
| Ex: 4x + 2x to get 6x |
4x + 2x = 6 to get x = 1 |
A solution of an equation is a number that, when
substituted for the variable, makes the equation true.
The solution is said to satisfy the equation.
Is x = -3 a solution of the equation 3x + 10 = 4 + x?
Is p = 7 a solution of the equation 5(p – 6) = -5?
Principles of Equality
Equivalent equations are equations that have the same solution.
2x + 6 = 14 and 2x = 8
x = 4
| Addition Principle of Equality |
| If a = b, then
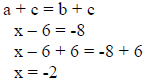 |
If x = 5, then x + 2 = 5 + 2
check:
 |
| Subtraction Principle of Equality |
If a = b, then
 |
If x = 5, then x – 2 = 5 - 2
check:
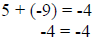
|
| Multiplication Principle of Equality |
| If a = b, then
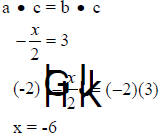 |
If x = 5, then 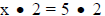
check:
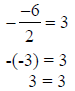
|
Combining Principles to Solve Linear Equations

Concept 2: Solving Equations II
Solving Linear Equations that contain Fractions
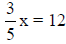 (show 2 ways) (show 2 ways)
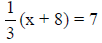
Solving Linear Equations that have Variables on both sides
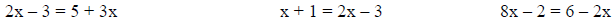
Solving Linear Equations that contain Parentheses

General Procedure for Solving a Linear Equation: pg.
152
1. If fractions are present, multiply both sides of the equation by the LCD of
all the fractions.
2. Simplify each side of the equation.
3. Use addition and subtraction to get all terms with the variable on one side
and all constant terms
on the other side of the equation. Then, simplify each side of the equation.
4. Divide both sides of the equation by the coefficient of the variable.
5. Check your solution in the original equation.
These problems have exactly one solution.
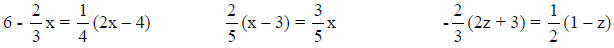
These problems have no solution
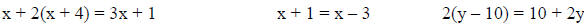
These problems have every value of the variable as a
solution. They are called an identity.

Review: When you solve a linear equation, if the
simplified equation is:
A false statement, such as 8 = 1, the equation has no solution.
A true statement, such as 12 = 12, the equation is an identity.
Any value of the variable is a solution.
A true statement, such as x = 4, there is only one solution.
FORMULAS:
d = rt, solve for r
ax + b = c, solve for x
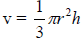 , for h , for h
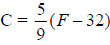 , for F , for F
8x – y = 5, for x
|