Solving Quadratic Equations by Completing the Square
Consider the equation
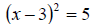
We can see clearly that the solutions are
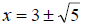
However,
What if the equation was given to us in standard form, that is
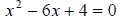
How would we go about solving the equation? What we want to do is change the
equation from standard form to the extracting roots form. That way we can easily
solve. To do this we use something called completing the square.
Completing the Square
To complete the square for the expression
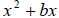 we add
we add
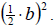 We get
We get
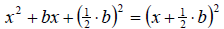
Notice that when we add this completing the square piece, we get a perfect
square trinomial. This will always be the case, therefore, we will always be
able to factor the expression once we have added in the expression
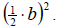
Example 1:
Complete the square on
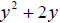 .
Then factor accordingly. .
Then factor accordingly.
Solution:
We simply add on the
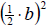 piece. In this case
piece. In this case
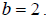 So we get
So we get
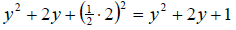
Factoring we get
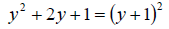
Notice that when we complete the square, the resulting trinomial will always
factor the same way. That is, (“variable” +/- “inside ( ) of completed square
piece”)2. We know if its + or – by taking the same sign as the original b value.
So example 1 we can visualize like the following
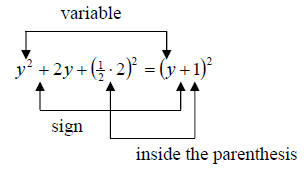
Again, when we complete the square it will always factor
like this. So we merely need to remember this pattern for more complicated
problems.
So we really want to use completing the square to solve
quadratic equations. To do that we first will notice a few things. To complete
the square, the leading coefficient must always be +1 as it is above (if its not
we can easily make it +1) and completing the square will work for any quadratic
equation. This means that we can always use completing the square as a technique
for solving.
Solving 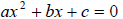 by Completing
the Square by Completing
the Square
1. Isolate the variable terms and make the leading
coefficient +1 by dividing each term by . a
2. To preserve the equality, add the expression
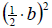 to both sides of the equation. to both sides of the equation.
3. Factor the variable side of the equation. It will always factor as a perfect
square.
4. Solve by extracting roots.
Example 2:
Solve the equations by completing the square.
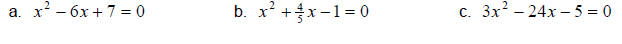
Solution:
a. To solve by completing the square we follow the steps above. We get

So the solution set is 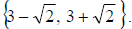
b. Again, we proceed as follows
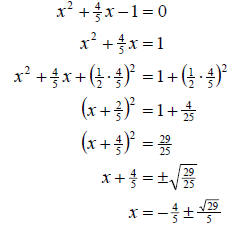
So the solution set is 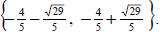
Note: The previous question shows us the advantage to
using the formula
(“variable” +/- “inside ( ) of completed square piece”)2 to factor
the trinomial portion. It simplifies the factoring which would have been much
more difficult in this case. So we can instead just remember the pattern and use
it to factor all completing the square problems no matter how difficult or
trivial.
c. Finally, we will again complete the square to solve.
However, this time we need to make sure the leading coefficient is +1. So, we
will start by dividing each term by 3 and then proceed as usual.

In the last step, the radical was simplified by
rationalizing the denominator.
So our solution set is 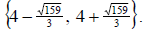
Now that we have the basic idea of completing the square,
lets see some examples which are a little more challenging.
Example 3:
Solve the equations by completing the square.

Solution:
a. The first thing we must do is write the equation in standard form. So we move
the terms around to get
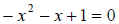
So in this equation its really easy to just start
completing the square without remembering that we need the leading coefficient
to be +1. It is currently –1. So we can fix that by multiplying the entire
equation by –1. We then proceed as normal.
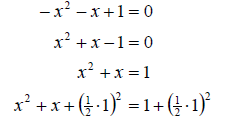

So our solution set is 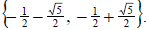
b. On this equation we need to again start by getting rid
of the parenthesis. Once we do that we can continue as normal
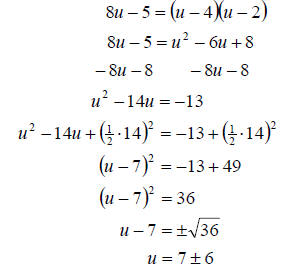
Notice that we can actually perform the operations of +
and – in the last step. Therefore, we must. So we have

So our solution set is 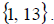
The fact that we got rational numbers in the answer of the
last example tells us that factoring could have been used to solve the quadratic
in that problem. However, since the instructions told us to solve by completing
the square, we had to solve using completing the square anyway.
10.2 Exercises
Complete the square on the following. Then factor accordingly.
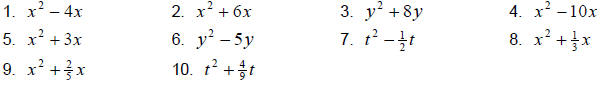
Solve the equations by completing the square.
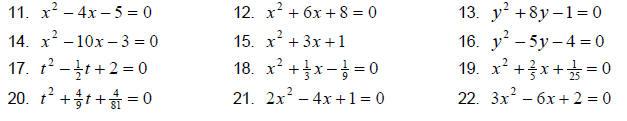
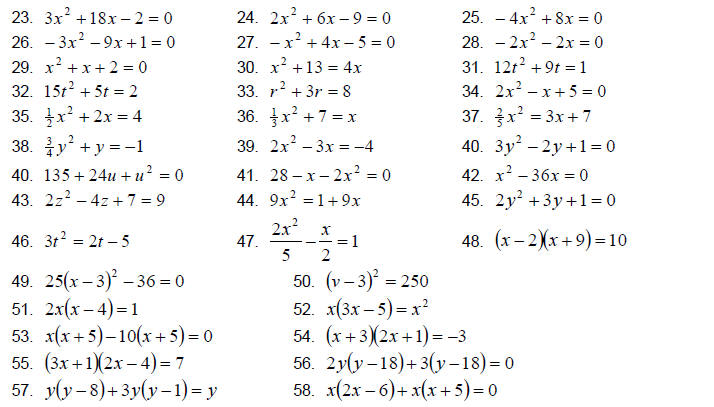
|