Solving Quadratic Equations

Using the square root property it is possible to solve any quadratic equation written in the form
( x + b )² = c . The key to setting these problems into the correct form is to recognize that
(x + b)² is a perfect square trinomial. To turn the equation given into one that can be solved using the square root property, the following must be done:

Given : ax² + bx + c = 0

1.) If a ≠ 1 divide both sides by a.
2.) Rewrite the equation so that both terms containing variables are on one side of the equation and the constant is on the other.
3.) Take half of the coefficient of x and square it.
4.) Add the square to both sides.
5.) One side should now be a perfect square trinomial.
Write it as the square of a binomial.
6.) Use the square root property to complete the solution.
 

Example 1. Solve 2a² – 4a – 5 = 0 by completing the square.

Solution
Step 1: Divide the equation by a

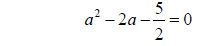
Step 2: Move the constant term to the right side of the equation

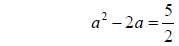
Step 3: Take half of the coefficient for x and square it

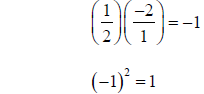
Step 4: Add the square to both sides of the equation

 

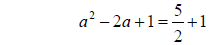
Example 1 (Continued):
Step 5: Factor the perfect square trinomial

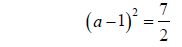
Step 6: Take the square root of both sides

 

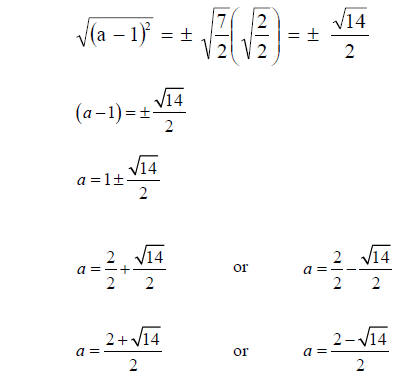
Example 2. Solve 9a²– 24a = -13 by completing the square.

Solution
Step 1: Divide the equation by a

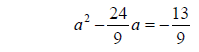
Step 2: Move the constant term to the right side of the equation

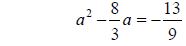
Example 2 (Continued):

Step 3: Take half of the coefficient for x and square it

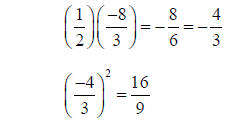
Step 4: Add the square to both sides of the equation

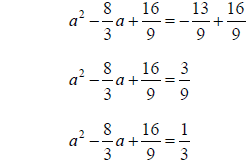
Step 5: Factor the perfect square trinomial

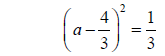
Step 6: Take the square root of both sides

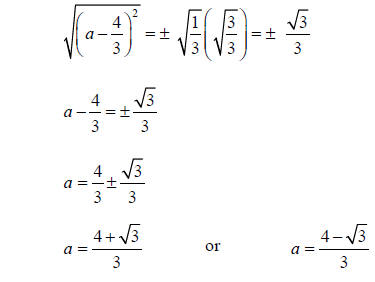
Example 3. Solve 9x² – 30x + 29 by completing the square.

Solution
Step 1: Divide the equation by a

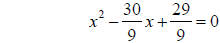
Step 2: Move the constant term to the right side of the equation

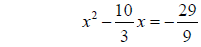
Step 3: Take half of the coefficient for x and square it

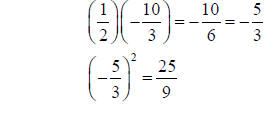
Step 4: Add the square to both sides of the equation

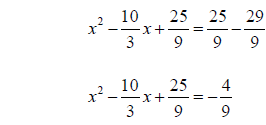
Step 5: Factor the perfect square trinomial

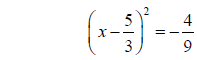
Example 3 (Continued):
Step 6: Take the square root of both sides
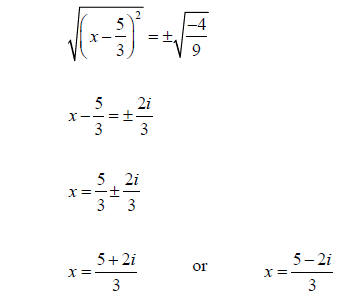