Summative Assessment of Problem-solving and Skills Outcomes

PART I: Problem-solving

Problem-solving Outcome: Students will use mathematical reasoning to solve problems and a
generalized problem solving process to work word problems.

Sampling design: From nine Math 25 sections taught by instructors participating in the Teaching
Community, we chose a random sample of three students from each section. The sample was taken
from students who were passing the course prior to taking the final exam. The sample contained 18
students. (Two of the eight instructors did not submit student work, so the sample did not contain
students from three sections.)

Method: We wrote four problems that met the criteria for problem-solving in the DE Problem-solving
Outcome. The four problems required students to apply concepts in a context, demonstrate conceptual
understanding, explain their reasoning, and use multiple approaches. The four problems were also
designed so that multiple strategies could lead to a solution; in this way, the problems were more than
standard word problems. Every instructor put these four problems on his/her final exam. (#2, 3, 7, and
17 from the common final exam)

Technique: All four problems from each student paper were assessed holistically using a rubric
written by the Teaching Community earlier in the semester. We began with a benchmarking exercise in
which each instructor graded the same three papers. We then discussed the scores on these three papers
and reached consensus. Next, each final was assessed independently by three instructors. If at least one
of the three scores differed from the mean of the three scores by more than 0.5, that student’s work was
discussed by the whole group until consensus was reached. Otherwise, scores were averaged.

Summary: See rubric for description of scores
Stemplot of rubric scores
2| 5 represents an average score of 2.5
Mean 3.6 Standard deviation .8
Quartiles: 2.5 3 3.5 4 5

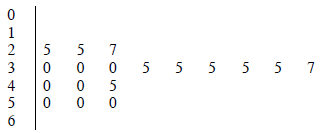
Student Profile Based On The Mean Rubric Score:
A mean score of 3.6 indicates that the average student in this sample can complete some important
components of the problem-solving task and communicate with sufficient clarity to get his/her idea
across. Portions of work may be unorganized or difficult to follow. Some strategies may be unclear or
inappropriate. At times, mathematical reasoning is not clear. There is evidence of applying relevant
concepts and appropriate processes throughout, though implementation is only partially successful in
some cases.

Observations: Instructors noted that nearly all students in the sample attempted every problem.
Uniformly, the students did a good job defining variables and using multiple approaches when
prompted. Very few papers explicitly demonstrated more sophisticated use of a general problem solving
process (e.g. stating givens and assumptions, giving estimates, checking). Generalizing other
weaknesses was more difficult. Instructors noted that frequently a student performed inconsistently on
the four problems, demonstrating good understanding in one setting and having difficulty with similar
concepts in another setting

Action: Instructors in the Teaching Community will focus more on problem-solving in fall 2003. The
use of computer-aided instruction to teach procedural algebra skills will provide more class time for
instructors to work on problem-solving and the other DE program learning outcomes. During the
summer session, eight instructors met for 3-hours a week to write and discuss classroom activities that
focus on conceptual development of algebra content and problem-solving. We will see if this increased
classroom focus on developing problem-solving skills improves student performance.

PART II: Skills Outcome

Skills Outcome: Students will recognize and apply math concepts in a variety of relevant settings and
demonstrate the math skills and knowledge necessary to succeed in subsequent courses.

Sampling design: From nine Math 25 sections taught by instructors participating in the Teaching
Community, we used all students who were passing the course prior to taking the final exam. The
sample contained 136 students from seven sections; 122 took the same final exam. (One instructor who
taught two sections did not submit data.)

Method: We identified six content objectives fundamental to Elementary Algebra. Using the common
final exam, we ranked problems (referenced in the table) by skill into three levels of difficulty. One
instructor gave a different final exam but ranked his problems similarly.

Technique: Instructors tallied the number of students who made minor errors and the number who got
the problem completely correct.

Level of Difficulty

Observations: In all skills at all levels of difficulty, over 69% of the students could either perform the
skill perfectly or with only minor errors. This sample of students had strengths in solving linear
equations (without fractions), finding the equation of a line from two points, and simplifying
polynomials. If we demand complete accuracy, we see weaknesses in solving linear equations with
fractions, finding equations of lines from verbal descriptions, solving linear inequalities, and using the
laws of exponents to simplify expressions. In all other skills at all levels of difficulty at least 50% of
the students performed the skill without errors.

Action: In an attempt to improve students’ procedural algebra skills, the Teaching Community is
experimenting with computer-aided instruction in fall 2003. With the PHIM-2 software, students will
be able to choose from a variety of instructional methods, receive immediate feedback, and work
problems until they reach mastery (defined as 85% correct in a given problem set). We will see if
computer-aided instruction improves students’ skills.