Solving Systems of Linear Equations In Three Variables

The solution to systems of equations to this point involved two-dimensional intersections of at least two lines. Recall that there were several possible outcomes:

 1.) Intersection at a single point (an ordered pair).
 2.) Infinite solutions because the lines were the same.
 3.) No solution because the lines were parallel.

In systems of linear equations in three variables the desired solution is an ordered triple (x, y, z) that exists in three-dimensional space. The best way to imagine this is to think of the point as a corner of a box.

The outcomes for these systems of equations are:

 1.) An intersection at one point (an ordered triple).
 2.) An infinite set of solutions (Dependent). This occurs when:
  a.) All three planes cross at a common line.
  b.) All three planes are the same.
 3.) No solution (Inconsistent). This occurs when:
  a.) Two or more of the planes are parallel and/or are cut by the third plane.
  b.) No planes are parallel but two intersect in a line that will be parallel to the third plane.

The following example will show a method to use to determine which of these outcomes results from the solving of the system. The key element to the procedure is the elimination-by-addition method covered previously.

NOTE: Not all problems will have an ordered triple as a solution!!

Example 1: Solve the following system of equations.

4x + 8y + z = 2
x + 7y – 3z = –14
2x – 3y + 2z = 3

Solution:

Step 1: Number the equations.

The equations are numbered to keep track of them during the solution process.
If this is not a problem for you than skip this step.

1) 4x + 8y + z = 2
2) x + 7y – 3z = –14
3) 2x – 3y + 2z = 3

Step 2: Determine a variable to eliminate.

Unless otherwise directed, select a variable that is easy to eliminate if any two
of the given equations are added together. Some helpful suggestions are
selecting a variable that is missing from one or more of the given equations or
one whose coefficient is one or finally one that appears as positive in one
equation and negative in another. For this example, z is selected.

Step 3: Create an equivalent equation or equations whose sum eliminates the
selected variable.

For this example equation 1 will be multiplied by the number three then added
to equation 2 to achieve a sum that has no z term.

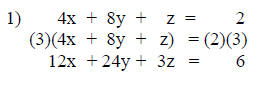
This is the equivalent equation 1 that is now added to equation 2. Their sum
will be known as equation 4.

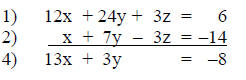
Step 4: The equation not used in step 3 (in this example equation 3) must now be
added to either equation 1 or 2 to eliminate the same variable. Use
equivalent equations if necessary.

In this example an equivalent equation of equation 1 will be used. This
equation is found by multiplying it by –2. The equation will then be added to
equation 3 to eliminate the z variable. The sum of these equations will be
known as equation 5.

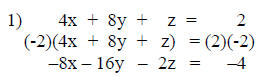
This is the equation equivalent to equation 1.

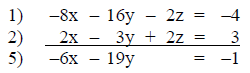
Step 5: Equations 4 and 5 are inspected to determine which variable can be
eliminated with the least amount of effort.

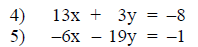
For this example, the x term will be selected. To obtain equivalent equations
whose sum will eliminate the x term, equation 4 is multiplied by six an
equation 5 by thirteen. The sum of these equations will be the value of the y
variable.

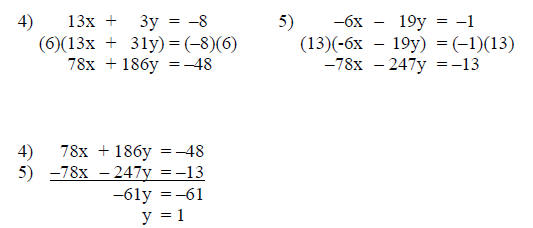
Step 6: Solve for a second variable.

The solution of a single variable in step 5 (for this example y = 1) is substituted
into either equation 4 or 5 to solve for the second variable. For this example,
equation 4 is used.

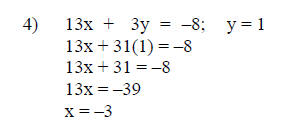
Step 7: Solve for the remaining variable

The solutions from steps 5 and 6 ( x = -3, y = 1 ) are substituted into either
equation 1, 2 or 3 to solve for the remaining variable, z in this case. Equation
1 will be used for this example.

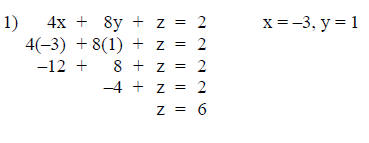
Step 8: Verify the solution set.

Substitute the solution from steps 5, 6 and 7 into both equations not used in
step 7 (in this case equations 2 and 3). This substitution must be made to
verify the type of outcome this system represents.

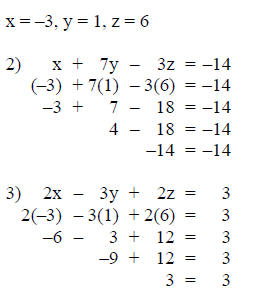
Since the solutions in step 8 are both true, the solution is an ordered triple
(-3, 1, 6).

If the outcome had been a false statement, such as 0 = 3, this would indicate an inconsistent system.

If, when finding an equivalent equation, one given equation is found to be the same as another, this represents a dependent system.